Introducción

La enseñanza de las matemáticas demanda una alta responsabilidad por parte de los estudiantes, pero también condiciones ambientales y didácticas en las respectivas instituciones escolares, donde la paciencia, tiempo y recursos son pilares esenciales. Realizar matemática no es repetir matemáticas ya hechas y descontextualizadas sino lograr un contacto estrecho entre quienes participan y la misma actividad.

Es necesario abandonar la idea de que los conceptos matemáticos duraderos son aquellos que se aprenden de memoria. El ser humano recuerda con mayor frecuencia y facilidad las ideas que él ha elaborado por sus propios medios y recursos, ayudado por métodos y la presencia permanente de los docentes (Mora, 2003).

Lo que enseña el docente no solo es lo relacionado a su disciplina, involucra prácticas discursivas, mediadas por creencias, actitudes y emociones. Las creencias hacia las matemáticas son subjetivas, derivadas de fantasías o experiencias, mientras que las actitudes y emociones se relacionan con una predisposición, positiva o negativa, que influye en el comportamiento y en las intenciones personales a través de aceptación o rechazo de la materia (Ruiz et al., 2011).

Las instituciones educativas que ligan a su currículo el uso de las Tecnologías de la Información y las Comunicaciones (TIC) como herramienta de aprendizaje, contribuyen a mejorar las competencias intelectuales a través de un aprendizaje significativo, modificando los paradigmas educativos convencionales (Barrios y Delgado, 2022)

Sánchez (2023) examina la evidencia sobre la incidencia del uso de software gamificado en el mejoramiento del rendimiento de los estudiantes, con una muestra de 66 estudiantes de bachillerato divididos en dos grupos, experimental y de control, concluyendo que la personalización en la gamificación son un punto crítico para lograr resultados consistentes. En tanto que Semanat y Robayo (2021) llevaron a cabo un estudio con 60 estudiantes de segundo año de bachillerato, precisando que la utilización de recursos tecnológicos en la enseñanza y aprendizaje de la matemática, beneficia la apropiación del conocimiento en el área de matemática. En ambos casos se concluyó, que la estrategia didáctica en TIC contribuyó a la adjudicación de conocimiento matemático dado que se obtuvieron experiencias significativas.

Villalón et al. (2020) expresan en su investigación, que la incorporación de las TIC en los procesos de enseñanza y aprendizaje promueve el desarrollo de la autonomía. Sin embargo, investigaciones desarrolladas por Quevedo y Erazo (2021) exponen la existencia de una brecha tecnológica entre los estudiantes y los docentes en torno al acceso del aprendizaje significativo para la asignatura de matemáticas. Por otra parte, Poyato (2021) manifiesta que el trabajo realizado con las herramientas digitales permite aumentar los tiempos de concentración y de trabajo, posibilitando un acercamiento autónomo a los contenidos matemáticos. De igual forma, Muñoz et al. (2020) concluyen que es necesario utilizar herramientas digitales que despierten el interés por aprender, fortaleciendo con ello el conocimiento y los procesos matemáticos.

En resumen, las formas de enseñar y aprender en la actualidad han sufrido cambios, los cuales responden a las necesidades de las actualizaciones curriculares principalmente y de manera secundaria a las insuficiencias que presentan los estudiantes al momento de instruirse. Las innovaciones que puedan darse están directamente relacionadas con el grado de comprensión de los recursos tecnológicos a la mano del propio estudiante y de la capacidad del docente por lograr trabajar en el mismo canal de comunicación. Precisamente, el presente trabajo rescata los resultados obtenidos tras poner en práctica el binomio de acción: mobile-learning y STEAM en grupos de matemáticas de bachillerato.

Marco teórico

Enseñar matemáticas a través de una idea inequívoca, formal y alejada de un entorno físico de aplicación es un enfoque totalmente tradicionalista o denominado conductista (Vesga y Falk, 2016); el profesor es el individuo que presenta sus conocimientos hacia el estudiantado, esperando que sea asimilado y replicado de manera mecánica dejando de lado la posibilidad de brindar tiempo y espacio suficiente para lograr el aprendizaje.

En contraparte existe un enfoque constructivista, donde el centro es el estudiante y la aplicación del conocimiento se hace en el mundo real. Existen concepciones erróneas en torno al constructivismo, como lo expresan algunos docentes, construir el conocimiento, es para ellos no involucrarse en el proceso sino proporcionar los insumos a los estudiantes y esperar que sean ellos quienes trabajen y lleguen a conclusiones (Ortiz, 2015).

Sin embargo, lo que se plantea en el constructivismo es una interacción entre el docente y el estudiante, cada uno expresando su conocimiento para alcanzar un aprendizaje significativo. Hein y Salett (2004) refuerzan la idea de Jiménez (2011), no basta tener conocimientos específicos sobre un asunto y ejercer su mera transmisión, es fundamental obtener nuevas habilidades en la aplicación y sociabilización de los conocimientos para que se alcance una mayor comprensión.

La enseñanza se caracteriza por ser un proceso activo, el cual requiere del dominio de la disciplina con conocimientos matemáticos básicos y rigurosos, necesarios para la comprensión del mundo de las matemáticas, pero además del dominio de un conjunto de habilidades y destrezas necesarias para un óptimo desempeño de la labor como docente de matemáticas (Mora, 2003). Así, Porlán (1995) explica cuatro tendencias didácticas, donde el profesor concibe la enseñanza y el aprendizaje de la matemática: tradicional, tecnológica, espontaneísta e investigativa (ver Tabla 1).

Tabla 1

Tendencias en el proceso de enseñanza aprendizaje matemática

Tendencia	Profesor	Estudiante	Aprendizaje
Tradicional	Exposición magistral	Adquisición de conceptos	Memoria como único recurso
Tecnológica	Elaboración de secuencias de aprendizaje	Ejecución de secuencias	Pruebas diagnósticas
Espontaneísta	Carácter formativo	Cambio actitudinal y adquisición de valores	Situaciones que propician el descubrimiento
Investigativa	Propuesta sobre el proceso de desarrollo por investigación.	Adquisición conceptos, procedimientos por investigación	Objetos de aprendizaje con significado

Entretanto, Yackel y Cobb (1996) precisan que las interacciones socio-matemáticas en el aula se pueden caracterizar en siete fases notoriamente identificadas en el proceso de aprendizaje y enseñanza de las matemáticas:

1) Introducción didáctica. Mención breve de la temática que se trabajará, así como el tiempo que durará.

2) Desarrollo de los contenidos matemáticos. El docente asume el control total de la clase y desarrolla nuevos contenidos.

3) Unidad de los conocimientos matemáticos. Asociación con el concepto de ideas fundamentales.

4) Consolidación de nuevos conocimientos matemáticos. Afianzamiento mediante repetición y ejercitación de los procedimientos y reglas.

5) Profundización de los conocimientos matemáticos. Ampliación en aspectos básicos y necesarios en correspondencia con intereses e inquietudes.

6) Inspección o evaluación de los nuevos conocimientos adquiridos. Canal adecuado para retroalimentar el proceso.

7) Corrección y eliminación de errores y concepciones erróneas. Se penalizan los errores, dejando de lado la posibilidad de conveniencia para un punto de partida.

Los docentes que logran identificar la necesidad de un cambio en la manera que presentan sus clases, están siendo críticos de las necesidades que se le presentan, es claro que ningún grupo es igual a otro, pero existen tendencias que pueden irse modificando con miras en una mejora continua, generando cambios en respuesta de las necesidades que los estudiantes solicitan.

Sistema Significativo

La teoría del aprendizaje significativo de Ausubel plantea que el aprendizaje del estudiante depende de la estructura cognitiva previa que se relaciona con la nueva información. Siendo la estructura cognitiva el conjunto de conceptos e ideas que un individuo posee en un determinado tema. (Ausubel, 1983). Debe considerarse lo que el estudiante conoce previamente para poder establecer una relación con lo que se aprenderá sino se estará generando un aprendizaje mecánico, al faltar la interacción entre conocimientos previos y futuros.

Carranza (2018), indica que para que el aprendizaje significativo pueda concretarse se requieren acciones en cada uno de los estudiantes, siendo estás:

Motivación. Compromiso del estudiante hacia el aprendizaje.
Comprensión. Relación entre contenido previo y el nuevo.
Funcionalidad. Utilización de los nuevos conocimientos adquiridos.
Participación activa. Estudio, análisis, discusión y elaboración de la información recibida.
Relación con la vida real. Aplicación de la información recibida para la solución de problemas –reales o posibles-.

El binomio de acción: mobile-learning y STEAM

Los dispositivos móviles brindan herramientas y recursos en cualquier momento y desde cualquier lugar, creándose una combinación de posibilidades que debidamente utilizadas pueden mejorar los resultados de aprendizaje, con la necesidad de conjugar modelos didácticos que permitan alcanzar el aprendizaje significativo en los estudiantes (Torres et al., 2015)

Cantú et al. (2019) precisan que las investigaciones generadas entorno a las TIC móviles han producido modelos de aprendizaje en ambientes móviles a pesar de los desafíos que genera la adaptación del uso de las TIC dentro y fuera del aula, además indica que el propósito del docente debe ser buscar y desarrollar nuevas estrategias que integren los procesos de enseñanza y aprendizaje móvil. Los modelos para el desarrollo de aprendizajes en contextos móviles son:

a) Modelo de Análisis Racional de la Educación Móvil (MARCO), propuesto por (Koole, 2009). Existen puntos de convergencia entre las TIC móviles, las capacidades de aprendizaje de los estudiantes y su interacción social del tipo heurístico.

b) Modelo de construcción de escenarios de aprendizaje móvil, propuesto por (Berking et al., 2012). Asimilación de contenidos y habilidades bajo esquemas de aprendizaje e instrucción.

c) Modelo de adopción de aprendizaje en contextos móviles, propuesto por (Udanor y Oparaku, 2016) Herramienta de apoyo al aula tradicional, mediante el uso de dispositivos.

d) Otros modelos de aprendizaje en contextos móviles. Educación Asistida por Ordenador.

La educación STEAM (Ciencia, Tecnología Ingeniería, Arte y Matemáticas) se basa en un aprendizaje que permite incentivar la solución de problemas, la colaboración, la innovación, la creatividad, la multidisciplinariedad, la toma de decisiones, el manejo y análisis de datos; además de fomentar la evaluación basada en resultados, y promover igualdad de género (Generación Anáhuac, 2019)

Las modificaciones propuestas, realizadas por el Colegio de Bachilleres de la Ciudad de México han sido poner en práctica estrategias metodológicas diferentes. Las cuales pretenden ayudar a los estudiantes a tener una asimilación de los contenidos por el uso de diferentes enfoques. Los estudiantes del Plantel 1 “El Rosario” presentan situaciones que complican su desarrollo en las asignaturas de Matemáticas.

Dentro de las principales dificultades, se encuentran la falta de competencias disciplinares básicas como formular y resolver problemas matemáticos, interpretar tablas y gráficos y argumentar soluciones mediante el lenguaje verbal matemático. Las competencias en la mayoría de la población estudiantil no se encuentran consolidadas contra una mínima proporción de estudiantes que logran tener una consolidación en ellas, las reuniones de Jornada Académica y de Gestión que programa el Colegio de Bachilleres de manera semestralmente permite abordar estos aspectos y caracterizar a los estudiantes.

El cambio en la forma de enseñanza de las matemáticas tendrá un impacto en la manera en que los estudiantes puedan aprender, considerando nuevas tendencias de acción, como es el uso de los teléfonos inteligentes para aplicar mobile-learning y la posibilidad de llevar a la práctica conocimientos matemáticos en un entorno inmediato a través de STEAM, las cuales buscan generar una mayor dinámica y como consecuencia desarrollar las competencias genéricas y disciplinares matemáticas, apoyados en el uso de metodologías que el Colegio de Bachilleres propone y además de un enfoque vivencial sobre la matemáticas y su entorno aplicativo.

La incorporación de las TIC a la enseñanza de las matemáticas a nivel media superior puede además ayudar a solventar situaciones concretas. Permitir al estudiante utilizar recursos que favorezcan aprendizajes de su propio semestre así como lograr consolidar aprendizajes que no fueron comprendidos con claridad de semestres previos.

Metodología

La investigación realizada se orientó hacia un estudio cualitativo-descriptivo empleando la investigación-acción. La investigación-acción toma como punto de partida el modelo cíclico que precisa tres momentos: identificación de una idea general cuyo propósito es mejorar o cambiar algún aspecto problemático de la práctica profesional, exploración o planteamiento de las hipótesis de acción como acciones que hay que realizar para cambiar la práctica y construcción del plan de acción, donde se realiza el proceso de revisión de la implementación y sus efectos así como el reconocimiento de posibles fallos y sus consecuencias (Latorre, 2005).

Figura 1

Ciclo de la investigación-acción.

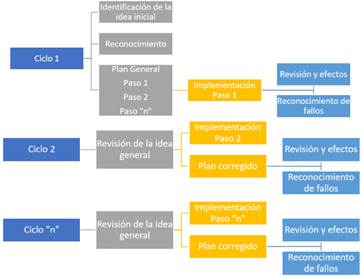
Nota: Elaboración propia con base en Latorre (2005)

La ejecución de un ciclo de investigación-acción no es suficiente, si se busca maximizar los resultados de mejora y cambio. Al respecto, Latorre (2005) expresa que “El tiempo necesario para que se origine el cambio dependerá de la frecuencia de las transacciones del profesorado con el alumnado, o de la capacidad que tenga el profesorado para analizar la situación problemática que intenta mejorar” (p.33).

Dentro del Colegio de Bachilleres de la Ciudad de México, Plantel 1 “El Rosario”, se llevó a cabo una intervención académica en el Semestre 2022 A y el Semestre 2022 B, comprendido entre el 21 de febrero de 2022 al 01 de julio de 2022 y entre el 05 de septiembre de 2022 al 13 de enero de 2023 respectivamente, con la intervención del binomio de acción: mobile-learning (a través del uso de la aplicación GeoGebra) y enfoque STEAM en un plan de acción de 8 fases, después de llevarse a cabo una Fase de Diagnóstico.

Figura 2

Plan de acción

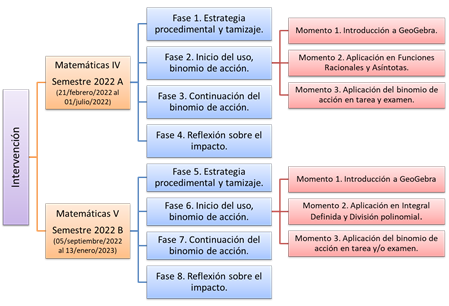Nota: Elaboración propia con base en Flores et al. (2020)

El avance del proceso de aprendizaje se evaluó considerando los factores contextuales relacionados con la entrega y cumplimiento de trabajos, la asistencia a las clases y la cantidad de semestres cursados en el Colegio por parte de los estudiantes. Para los factores de entrada, las herramientas con las que conto la Institución (toma de corriente eléctrica, laptops y proyectores), herramientas individuales –teléfono móvil- y la capacitación de docentes en aplicaciones fue crucial.

En tanto que los factores de proceso se ligan con la interacción estudiante-docente, considerando un canal de comunicación abierto y estable para generar una mayor sinergia. Finalmente, los factores de producto se valoran con el desarrollo de las competencias matemáticas de los estudiantes. Los criterios de la evaluación se reflejan en la Tabla 2.

Tabla 2.

Criterios de Evaluación

Factor	Evaluación	Binomio de acción
Contextual	Cumplimiento de asistencia y trabajos	Porcentaje de ausentismo y reprobación
De entrada	Uso de recursos tecnológicos	Grado de manejo de dispositivo móvil con aplicación GeoGebra
De proceso	Interacción estudiante-docente	Viabilidad de seguir con el desarrollo del proyecto por la intervención del binomio de acción.
De producto	Desarrollo de las competencias matemáticas	Ponderación del grado de desarrollo de las competencias matemáticas del grado cursado.

Resultados y discusión

El cambio en la forma de enseñanza de las matemáticas tuvo un impacto en la manera en que los estudiantes pudieron aprender, considerando nuevas tendencias de acción, como es el uso de los teléfonos inteligentes para aplicar mobile-learning y la posibilidad de llevar a la práctica conocimientos matemáticos en un entorno inmediato a través de STEAM, los cuales buscaron generar una mayor dinámica y como consecuencia desarrollar las competencias matemáticas, apoyados en el uso de metodologías que el Colegio de Bachilleres propone y además de un enfoque vivencial sobre las matemáticas y su entorno aplicativo

Tabla 3

Distribución de grupos a conveniencia

Semestre	Grupo	Total de estudiantes inscritos	Ausentes
Cuarto	452	40	4
Quinto	552	31	2
Quinto	564	40	7

Experiencias cualitativas

En el grupo 452, los estudiantes coinciden en la necesidad de recibir una enseñanza procedimental, así como el uso del pizarrón como herramienta imprescindible. Siendo sujetos partícipes del proceso de enseñanza aprendizaje y no solo entes receptores, considerando el trabajo en equipos y no solo de manera individual. El uso de dispositivos móviles genera un cambio de paradigma ante el proceso tradicionalista habitual dentro del Colegio de Bachilleres, al cual están acostumbrados los estudiantes.

El análisis proporcionado por algunos estudiantes resalta un límite que debe existir entre: mobile-learning y el aprendizaje tradicionalista, “la aplicación debe ser usada en algunas ocasiones, para evitar que haga todo por nosotros”. Lo cual permite precisar que los estudiantes son conscientes, sobre la necesidad de desarrollar de manera individual competencias matemáticas.

Para los grupos 552 y 564, la posibilidad de contar con una herramienta que los guie en el desarrollo de los ejercicios asignados, trae consigo un sentimiento de tranquilidad y esperanza, pues les resulta importante poder saber si el desarrollo parcial tiene un sentido algebraicamente correcto; coinciden en la necesidad de usar aplicaciones que permitan subsanar competencias que aún no están consolidadas, como lo es GeoGebra.

La mayoría de los estudiantes reconoce la importancia de poder contrastar el resultado final obtenido de manera personal con el expuesto por la aplicación, “en ocasiones me confundí, pero en la mayoría de las veces cuando confirmé mi resultado fue demasiado útil”. Lo cual habla de una transición del sistema tradicional hacia un sistema significativo, el tiempo de desapego conllevara una reestructuración desde asignaturas previas a nivel bachillerato y en un punto a largo plazo desde niveles básicos.

Experiencias cuantitativas

Los aspectos cuantitativos de análisis se abocaron a tres puntos clave, Fase 2 y Fase 6 del plan de acción, el primero de ellos sobre la aplicación del conocimiento sobre GeoGebra en la asignatura cursada o anteriores, el segundo punto sobre la dificultad de la ejecución de la aplicación y finalmente sobre el alcance en futuros periodos de evaluación, como se observa en la Tabla 4.

Tabla 4

Aplicación del binomio de acción

Punto 1		Si, lo utilice en otras materias	Sí, pero nunca lo use	No la conocía
¿Conocía el Software GeoGebra antes de usarlo en la asignatura de Matemáticas?	452	12%	19%	69%
	552	45%	24%	31%
	564	9%	36%	55%
Punto 2		Fue fácil e intuitivo	Fue fácil pero no intuitivo	Fue intuitivo pero no fácil	No fue fácil y tampoco intuitivo
¿Le resulto fácil e intuitivo usar la aplicación?	452	83%	6%	8%	3%
	552	55%	14%	31%	0%
	564	52%	18%	24%	6%
Punto 3		Si	No	Tal vez
Le gustaría que el uso de GeoGebra se mantenga para el tercer parcial de Matemáticas	452	89%	3%	8%
	552	86%	0%	14%
	564	91%	0%	9%

Es posible observar que en el punto 1, los grupos 452 y 564 no conocían el Software GeoGebra en su mayoría, el grupo 552 indica que solo 1 de cada tres estudiantes. Para el punto 2, los tres grupos indican que les resulto fácil e intuitivo en un porcentaje mayoritario. Finalmente, para el punto 3, los grupos por unanimidad precisan que les gustaría que se mantenga el uso para el tercer parcial. Existe una homogeneidad en cuanto al desconocimiento de la aplicación, así como los beneficios que aporta; sobre lo fácil que resulta usarla y sobre la continuidad que permite el desarrollo de las competencias matemáticas a lo largo del curso.

Para las Fases 3 y 7 del plan de acción, se logró identificar el grado de competencias matemáticas alcanzadas en cada grupo, clasificadas en Consolidada, En Desarrollo y No Consolidada, la primera de ellas corresponde a estudiantes que lograron adquirir las competencias del semestre en curso y que además cuentan con habilidades del semestre anterior; la segunda indica que existe un trabajo por desarrollar, como consecuencia de competencias en vías de mejora del semestre anterior o en curso; la tercera y última clasificación indica que no se han logrado desarrollar las competencias matemáticas de semestres previos ni del curso en cuestión

En el grupo 452 el nivel de consolidación promedio es de 46%, el nivel de competencia en desarrollo de 25% y de no consolidación 29%. Para el grupo 552, el 36% del grupo consolido las competencias, 34% presenta desarrollo y 30% no logro la consolidación. Por último, el grupo 564, presenta el 48% de estudiantes con una consolidación de la competencia matemática, el 37% se encuentra en vías del desarrollo matemático y el 15% no logra una consolidación.

Lo anterior pone de manifiesto un porcentaje mayoritario de consolidación en cada grupo intervenido, en términos binarios, para el grupo 452, 7 cada 10 estudiantes presentan una consolidación o desarrollo de las competencias: identificar un intervalo creciente o decreciente, determinar asíntotas verticales u horizontales, derivar funciones básicas y obtener máximos y/o mínimos de una función. Para el grupo 552, la cuantificación es la misma, 7 de cada 10 estudiantes presentan una consolidación o desarrollo de las competencias, pero en los temas: aproximar el área de una curva con rectángulos, calcular el área de una curva con integrales definidas, encontrar la antiderivada de una función polinomial y resolver integrales por método de integración por partes. Finalmente, en el grupo 564, 8 de cada 10 estudiantes presentan una consolidación o desarrollo de las competencias, en temas del semestre quinto de matemáticas.

En la Tabla 5, se muestran los porcentajes finales semestrales de la asignatura de Matemáticas IV Cálculo Diferencial, con un 90% de aprobación, 0% de reprobación y 10% de ausentismo. Existiendo un aumento del 23% con respecto al histórico de aprobación registrada, disminución del 100% en reprobación y 48% en ausentismo respecto al histórico. Traduciéndose en la recomendación de realizar sin cambios de inicio a fin, el desarrollo de la ruta de intervención binomio de acción: mobile-learning y STEAM. A su vez la asignatura de Matemáticas V obtuvo un 84% de aprobación, 10% de reprobación y un 6% de ausentismo para la Intervención A, la cual constó de dos semestres continuos del binomio de acción; existiendo un aumento del 40% con respecto al histórico de aprobación registrada, disminución del 9% en reprobación y 79% en ausentismo respecto al histórico. Para la Intervención B, el cual tuvo un semestre de intervención con el binomio de acción, los resultados fueron de un 78% de aprobación, 2% de reprobación y 20% de ausentismo, lo que representa un aumento del 30% con respecto al histórico de aprobados, un 80% de disminución en reprobados y un 31% de depreciación en el ausentismo.

Tabla 5

Porcentajes históricos vs Porcentajes con intervención Matemáticas IV y V

	Aprobados	Reprobados	Ausentes
Matemáticas IV “Histórico”	73%	8%	19%
Matemáticas IV “Intervención”	90%	0%	10%
Matemáticas V “Histórico”	60%	11%	29%
Matemáticas V “Intervención A”	84%	10%	6%
Matemáticas V “Intervención B”	78%	2%	20%

Traduciéndose en la recomendación de realizar sin cambios de inicio a fin, el desarrollo de la ruta de intervención binomio de acción: mobile-learning y STEAM para la Intervención A y la Intervención B, cada una con sus respectivas áreas de oportunidades, puntos clave de desarrollo y eficiencias obtenidas dado el tiempo de intervención.

Finalmente, se concluye que las variables, enseñanza con el binomio de acción y los resultados académicos indicaron un comportamiento dependiente e independiente después de realizar una prueba exacta de Fisher, se consideró una hipótesis nula -variables independientes- y una hipótesis alternativa –variables dependientes-, con un nivel de significancia α=0.05 traduciéndose en un nivel de confianza del 95%.

Para el grupo 452, el valor de p es de 0.0296, lo cual permite decir que p< α, rechazando la hipótesis nula; determinando que las variables son dependientes, el tipo de enseñanza impacta en los porcentajes académicos, no siendo un evento azaroso. En el grupo 552, el valor de p es 0.0043, lo cual tiene una interpretación análoga al grupo 452, las variables son dependientes. En este punto se puede decir que el efecto del binomio de acción va más allá de solo permitir que el estudiante desarrolle sus competencias matemáticas, el impacto que tiene permite una valoración de mayor acreditación en contraste con una enseñanza procedimental, lo cual repercute además en la reducción de los niveles de reprobación y ausentismo.

Si bien para dos grupos la dependencia de las variables es evidente, no lo es así para el grupo 564, el valor de p es de 0.0527, lo que impide rechazar la hipótesis nula, dando como conclusión que las variables son independientes. De dos grupos de Matemáticas V intervenidos con el binomio de acción, uno no tiene dependencia en las variables y el otro si, esto se ha comprendido de la siguiente manera, el grupo 552 tuvo 16 estudiantes que habían ya trabajado con la intervención y tuvieron un lapso de tiempo mayor, un año, en comparación con el grupo 564 donde no se tenía previo trabajo académico, partiendo de un tiempo cero y llegando solamente a medio año de intervención.

Para el factor de entrada, manejo del dispositivo, se presenta un porcentaje mayoritario en los tres grupos, 83% en el 452, 55% en el 552 y 52% en el 564, lo cual genera un grado de admisión sobre la estrategia de trabajo académico. En el factor de proceso se tiene un promedio para los tres grupos, del 89%, los estudiantes consideran conveniente seguir usando la aplicación en su dispositivo móvil, lo cual permite considerar con éxito el desarrollo de la estrategia de intervención, binomio de acción.

Por último, en el factor de producto desde un contexto dicotómico, 10 de cada 36 estudiantes no logró un avance académico contra 26 de cada 36 estudiantes que se encuentran en proceso y/o logro integral en el grupo 452. Para el grupo 552 se tiene un balance 24 de cada 29 estudiantes a favor de una correcta consolidación en tanto que 5 de cada 29 tiene un área de trabajo específico, mientras que en el grupo 564, 26 de cada 33 estudiantes tienen una consolidación o desarrollo de las competencias matemática, contra 7 de cada 33 que no lo logró.

Conclusiones

La ejecución de la estrategia de intervención, binomio de acción es aceptada por los estudiantes loa que mostraron una prestancia hacia estrategias de enseñanza aprendizaje no tradicionales, sin embargo, aun necesitan alcanzar una enseñanza procedimental operativa, abriendo la posibilidad de considerar un tiempo de transición, entre el sistema tradicional y el significativo, de mínimo dos semestres de forma continua.

El ausentismo académico disminuye, al igual que el porcentaje de reprobación de manera variable, pero en cualquier caso se justifica por el nivel de aceptación de los estudiantes y la forma de presentar la alternativa académica por parte del docente a cargo del grupo. El nivel de aprobación aumenta un 19% con respecto al histórico de grupos de Cálculo Diferencial y Cálculo Integral.

El software GeoGebra es una herramienta de verificación algebraica y gráfica para el estudiante, que le permite confiar en sus habilidades matemáticas y potencializa la posibilidad de ir desarrollando las competencias matemáticas. Para el docente resulta ser un soporte operativo, el cual permite mostrar al estudiante temas previos, consolidados o no, que permiten construir el conocimiento nuevo.

Se recomienda continuar con una investigación en las asignaturas de Matemáticas I, II y III, para lograr precisar el impacto que tiene el binomio de acción en las ramas de las Matemáticas a nivel bachillerato, así como el grado de entendimiento que se logre en la rama: Cálculo Diferencial e Integral, dada una preparación previa orientada y focalizada.

Referencias

Ausubel, D. (1983). Teoría del aprendizaje significativo. Fascículos del CEIF.

Barrios, S. y Delgado, G. (2022). Efectos de los recursos tecnológicos en el aprendizaje de las matematicas. Revista Digital: Matemática, Educación e Internet, 22(1). 1-14. https://doi.org/10.18845/rdmei.v22i1.5731

Berking, P., Haag, J., Archivald, T. y Birtwhistle, M. (2012). Aprendizaje móvil: no sólo otro método de entrega. http://www.vacolab.adlnet.org/wp-content/uploads/2012/12/12079.pdf

Carranza, A. M. (2018). Enseñanza y aprendizaje significativo en una modalidad mixta: percepciones de docentes y estudiantes. Revista Iberoamericana para la Investigación y el Desarrollo Educativo, 8(15), 898-922. https://doi.org/10.23913/ride.v8i15.326

Cantú, D., Amaya, A. y Baca, J. R. (2019). Modelo para el refuerzo del aprendizaje con dispositivos móviles. Ciencia UAT, 13 (2),56-70. https://www.redalyc.org/articulo.oa?id=441960176005

Flores, L.G., Veytia, M.G. y Moreno Tapia, J., (2020). Clase invertida para el desarrollo de la competencia: uso de la tecnología en estudiantes de preparatoria. Revista Educación. 44(1), 1-30 https://doi.org/10.15517/revedu.v44i1.36961

Generación Anáhuac. (2019). La importancia de las STEAM en la educación. Obtenido de Red de universidades Anáhuac: https://www.anahuac.mx/generacion-anahuac/la-importancia-de-las-steam-en-la-educacion

Koole, M. (2009). Un modelo para enmarcar el aprendizaje móvil. Athabasca. https://auspace.athabascau.ca/bitstream/handle/2149/2016/02_Mohamed_Ally_2009Article2.pdf;jsessionid=803E45D385C168F3E4E5F3B3817A98F9?sequence=1

Hein, N. y Salett, M. (2004). Modelación matemática y los desafíos para enseñar matemática. Educación Matemática, 16 (2) ,105-125. https://www.redalyc.org/articulo.oa?id=40516206

Jiménez, E. A. (2011). La naturaleza de la Matemática, sus concepciones y su influencia en el salón de clase. Educación y Ciencia, (13). https://doi.org/10.19053/01207105.765

Latorre, A. (2005) La investigación-acción. Conocer y cambiar la práctica educativa. Graó. https://www.uv.mx/rmipe/files/2019/07/La-investigacion-accion-conocer-y-cambiar-la-practica-educativa.pdf

Mora, C., D. (2003). Estrategias para el aprendizaje y la enseñanza de las matemáticas. Revista de Pedagogía, 24(70), 181-272 http://ve.scielo.org/scielo.php?script=sci_arttext&pid=S0798-97922003000200002 .

Muñoz, I., García, D., Mena, S. y Erazo, J. (2020). Enseñanza matemática: Uso de recursos digitales. Revista Koinonía, 5(1), 793-814. http://dx.doi.org/10.35381/r.k.v5i1.810

Ortiz, G. D. (2015). El constructivismo como teoría y método de enseñanza. Sophia: colección de Filosofía de la Educación, 19 (2), pp. 93-110. https://doi.org/10.17163/soph.n19.2015.04

Poyato, L, F. (2021) Relación entre motivación por las matemáticas y aprendizaje activo a través de herramientas digitales. Epsilón, 107, 59-65. https://thales.cica.es/epsilon/sites/thales.cica.es.epsilon/files/epsilon107_5.pdf

Quevedo, G.M. y Erazo, J. C., (2021). Plataformas digitales para la enseñanza de Matemáticas en básica superior. Revista Koinonia, 6(3), 494-509 http://dx.doi.org/10.35381/r.k.v6i3.1327

Ruiz, M., D., García, M., Peña, P. y Ruiz, H. (2011). Representaciones sociales en el aprendizaje de la matematica. Educere, 15 (51), 439-449 https://www.redalyc.org/articulo.oa?id=35621559014

Sánchez, C. (2023). Las competencias matemáticas y el empleo de las tecnologías en estudiantes de bachillerato en México. Revista Varela, 23(64), 24-37. https://revistavarela.uclv.edu.cu/index.php/rv/article/view/1472

Semanate, D. E. y Robayo, D.J. (2021). Estrategia didáctica basada en TIC para mejorar el desempeño académico en el área de Matemática. Episteme koinonia, 4(8), 379-403. http://dx.doi.org/10.35381/e.k.v4i8.1384

Torres, D., Infante, M., y Torres C. (2015). Aprendizaje móvil: perspectivas. RUSC. Universities and Knowledge Society Journal, 12(1), 38-49. https://www.redalyc.org/articulo.oa?id=78033494005

Udanor, C. & Oparaku, O. (2016). A performance evaluation of a multi-agent mobile learning system. International Journal of Interactive MobileTechnologies. 10(2), 10-18. https://www.researchgate.net/publication/301713898_A_Performance_Evaluation_of_a_Multi-Agent_Mobile_Learning_System

Vesga, G. y Falk, M. (2016). Creencias epistemológicas de docentes de matemáticas acerca de la matemática, su enseñanza y su relación con la práctica docente. Revista Papeles, 8(16), 11-25. https://core.ac.uk/download/pdf/236384102.pdf

Villalón, G., Cisneros, L., Medina, T., Sillero, P., J.A. y Vaca, G., (2020). Acompañamiento académico a estudiantes del nivel medio superior. Pistas Educativas, 42(136) ,148-162. http://www.itc.mx/ojs/index.php/pistas/article/view/2479

Yackel, E. y Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education. 27 (4). 458-477. https://www.jstor.org/stable/749877?origin=JSTOR-pdf